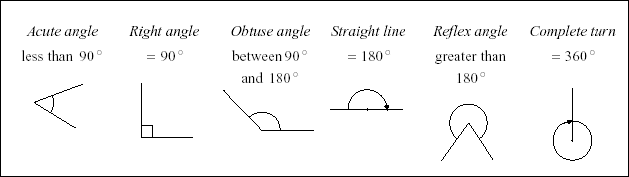GREATEST COMMON FACTOR (GCF)
OBJECTIVES
- Find the greatest common factor (GCF) of numbers
- Find he GCF of terms
- Factor out the GCF
- Factor a four-term expression by grouping
GETTING STARTED
- Product and Factors
15 = 3 x 5
15 is product
13 and 5 are factors
Factoring completely means to have all factors as prime numbers.
another example is 20 = 2 x 2 x 5
FINDING THE GREATEST COMMON FACTOR (GCF) OF NUMBERS
- The GCF of a list of integers is the largest common factor of the integers in the list.
Example 45 = 3 x 3 x 5 = 3^2 x 5
60 = 2^2 x 3 x 5
- To find the GCF, choose prime factors with the smallest exponents and find their product.
the same factors are 3 and 5, then the smallest exponent is 1. So, we can choose 3 and 5 and multiply it.
3 x 5 = 15
15 is the greatest common factor (GCF) of 45 and 60
Once again ...
- To find the GCF, choose prime factors with the smallest exponents and find their product.
36, 60, 108
36 = 2^2 x 3^2
60 = 2^2 x 3 x 5
108 = 2^2 x 3^3
Then, 2^2 x 3 = 12
So, 12 the greatest common factor (GCF) of 36, 60, dan 108
Another way to solve it ...
2 | 36 60 108
2 | 18 30 54
3 | 9 15 27
3 5 9
Collect the terms, that are 2 x 2 x 3 = 12
Then, we get the same result.
-----------------------------------------------------------------------------------------------------------------
THE CHARACTERISTICS OF NUMBER
PROPERTIES OF NUMBERS
- The Reflexive Property of Equality
A number is equal to itself.
symbolicly is A = A
Example 2 same as 2
- The Symmetric Property of Equality
If one value is equal to another, then that second value is the sameas the first.
symbolicly is A = B then B = A
example 3 = x
so, x = 3
- The Transitive Property of Equality
If one value is equal to a second, and the second happens to bethe same as a third, then we can conclude the first value must also equal the third.
symbolicly A = B and B = C, so, A = C
- The Substitution Property
If one value is equal toanother, then the secondvaluecan be used in place of the firstin any algebraic expression dealing with the first value.
- The Additive Property of Equality
We can add equal values to both sides of an equation without changing the validity of the equation.
A = B
A + C = B + C
C + A = C + B
- The Cancellation Law of Additive
A + C = B + C
if we will cancel the substitution, we just substract -C
then A + C - C = B + C - C can be A = B
- The Multiplicative Property of Equality
We can multiply equal values to both sides of an equation without changing the validity of the equation.
A = B
A x C = B x C
C x A = C x B
- The Cancellation Law of Multiplication
A x C = B x C
if we wanna cancel the C, so, we just divide both sides with C and C is not zero
A = B
- The Zero-FactorProperty
If two values that are being multiplied together equal zero, then one of the values, or both of them, must equal zero.
AB = 0
A = 0 or B = 0 or A and B = 0
PROPERTIES OF INEQUALITY
- The Law of Trichotomy
For any two values, only one of the following can be true about these values:
They are equal. The first has a smaller value than the second. The first has a larger value than the second.
Given any numbers A and B
that can be A = B or A < B or A > B
- The Transitive Property of Inequality
If one value is smaller than a second, and the second is less than a third, then we can conclude the first value is smaller than the third.
A < B and B < C so, A < C
PROPERTIES OF ABSOLUTE VALUE
|A| >= 0
|-A| = |A|
|AxB| = |A| x |B|
|A/B| = |A| / |B|
B is not zero
PROPERTIES OF NUMBERS
CLOSURE
- The Closure Property of Addition
When you add real numbers to other real numbers, the sum is also real.
Addition is a "closed" operation.
A + B = real numbers
A is real number
B is real number
The result is real
- The Closure Property of Multiplication
When you multiply real numbers to other real numbers, the product is a real number.
Multiplication is a "closed" operation.
A x B = real number
A is real number
B is real number
The result is real
- A Special Note
Substraction operation is not "closed"operation. Example: 3 - 5 = -2
3 is natural number and 5 is natural number, but the result is -2 and its is not a natural number. So, substraction operation is not "closed"operation.
COMMUTATIVE
-The Commutative Property of Addition
It does not matter the order in which numbers are added together.
A + B <--> B + A
-The Commutative Property of Multiplication
It does not matter the order in which numbers are multiplied together.
A x B <--> B x A
ASSOCIATIVITY
-The Associative Property of Addition
When we wish to add three (or more) numbers. It does not matter how we group them together for adding purposes. The parentheses ca be placed as we wish.
(A + B) + C
A + (B + C)
-The Associative Property of Multiplication
When we wish to multiply three (or more) numbers. It does not matter how we group them together for multiplication purposes. The parentheses ca be placed as we wish.
(A x B) x C
A x (B x C)
- By the way ...
It does not valid in substraction and division.
IDENTITY
-The Identity Property of Multiplication
There exists a special number, called the "additive identity", when added to any other number, then that other number will still "keep its identity" and remain the same.
A + 0 = A <--> 0 + A = A (a number plus zero still that number)
-The Identity Property of Multiplication
There exists a special number, called the "multiplicative identity", when multiplied to any other number, then that other number will still "keep its identity" and remain the same.
A x 1 = A <--> 1 x A = A (a number plus zero still that number)
INVERSE
- The Inverse Property of Addition
For every real number, there exists another real number that is called its opposite, such that, when added together, you get the additive identity (the number zero).
A + (-A) = 0
(-A) + A = 0
So, -A is an opposite of A
- The Inverse Property of Multiplication
For every real number, except zero. there exists another real number that is called its multiplicative inverse, or reciprocal, such that, when multiplied together, you get the multiplicative identity (the number one).
A x 1/A = 1
1/A x A = 1
DISTRIBUTIVITY
- The Distributive Law of Multiplication Over Addition
Multipling a number by a sum of numbers is the same asmultiplying each numberinthe sum individually, then adding up our products.
Example:
5 (7 + 3) = 5 (10) = 50
5 (7) + 5 (3) = 35 + 15 = 50
the result is same
So, A (B + C) = AB + AC
(A + B) C = AC + BC
- The Distributive Law of Multiplication Over Subtraction
A (B - C) = AB - AC
- The General Distributive Property
a (b1+b2+b3+...+bn) = ab1 + ab2 + ab3 +...+ abn
2 (1+3+5+7) = 2 + 6 + 10 + 14 = 32
- The Negation Distributive Property
If you negate (or find the opposite) of a sum, just "change the signs" of whatever is inside the parentheses.
-(A+B) = (-A) + (-B) = - A - B
-----------------------------------------------------------------------------------------------------------------
PRE_CALCULUS
Graph of a Rational Function
Given f(x) = (x+2) / (x-1)
if x=1 then can be 3/0 and the result is can not be define
if we draw in the graph, it will break the graph
So, we must substitute x with number except 1
if x = -3, f(-3) = 1/4
x = -2, f(-2) = 0
x = -1, f(-1) = -1/2
x = 0, f(0) = -2
x = 2, f(2) = 4
x = 3, f(3) = 5/2
Then, the graph is
Minggu, 15 April 2012
Minggu, 08 April 2012
REFLECTION OF MY LESSON
An angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Initial side of an angle is the ray where measurement of an angle starts. Terminal side of an angle is the ray where measurement of an angle stops.

Parts of an Angle

The corner point of an angle is called the vertex and the two straight sides are called arms. The angle is the amount of turn between each arm.
Type of Angle Description
Acute Angle an angle that is less than 90°
Right Angle an angle that is 90° exactly
Obtuse Angle an angle that is greater than 90° but less than 180°
Straight Angle an angle that is 180° exactly
Reflex Angle an angle that is greater than 180°
Positive and Negative Angle
The angle is measured by the amount of rotation from the initial side to the terminal side. If measured in a counterclockwise direction the measurement is positive (called positive angle). If measured in a clockwise direction the measurement is negative (called negative angle). (A negative associated with an angle's measure refers to its "direction" of measurement, clockwise.)

Standard Position

An angle is in standard position if its vertex is located at the origin and one ray is on the positive x-axis. The ray on the x-axis is called the initial side and the other ray is called the terminal side. If the terminal side of an angle lies "on" the axes (such as 0º, 90º, 180º, 270º, 360º ), it is called a quadrantal angle. The angle shown at the right is referred to as a Quadrant II angle since its terminal side lies in Quadrant II.
Special angle : 0°, 30°, 45°, 60°, and 90°
DEGREES AND RADIANS
Degrees
We can measure Angles in Degrees.
There are 360 degrees in one Full Rotation (one complete circle around). A Full Circle is 360°.
One complete turn (360°) is equal to 2π radians, so 180° is equal to π radians, or equivalently, the degree is a mathematical constant: 1° = π⁄180.
The Degree Symbol: °
We use a little circle ° following the number to mean degrees. For example 90° means 90 degrees.
Radians
We can measure Angles in Radians.
1 Radian is about 57.2958 degrees. Radian is a pure measure based on the Radius of the circle.
Radians and Degrees
There are π radians in a half circle
And also 180° in a half circle
So π radians = 180°
So, 1 radian = 180°/π = 57.2958° (approximately)
Degrees Radians Radians
(exact) (approx)
0° 0 0
30° π/6 0.524
45° π/4 0.785
60° π/3 1.047
90° π/2 1.571
180° π 3.142
270° 3π/2 4.712
360° 2π 6.283
How to convert
360° = 2π
360° / 2 = 2π / 2
180° / 180° = π / 180°
1° = π / 180°
and
2π radian = 360°
2π radian / 2π = 360° / 2π
1 radians = 180° / π
Example
120° = ... radians
120° = 120° x π/180 radians
= 2/3 π
11/12 π rad = ... °
11/12 π = 180°/π x 11/12 π
= 165°
MULTIPLYING EXPONENTS
There are some rules to solve exponent problems:
Rule 1

If the bases are different but the exponents are the same, then we can combine them.
Example 3^5 x 4^5 = (3 x 4)^5 = 125 = 248832
Rule 2

Dividing different bases can’t be simplified unless the exponents are equal. So, we can divide bases, then count its exponent.
Example 6^3 / 3^3 = (6/3)^3 = 3^3 = 27
Rule 3

We just multiply the exponents.
Example (23)^2 = (2 x 2 x 2)^2 = 8^2 = 64 = 2^6
(23)^2 = (2)^(3x2) = 2^6 = 64
Rule 4

When the bases are the same, then, just adding the exponents.
Example 2^3 x 2^5 = 2^(3+5) = 2^8 = 256
Rule 5

For division with same bases, then subtract exponents.
Example 4^5 / 4^3 = 4^(5-3) = 4^2 = 16
MULTI DIVISION MATH
How to calculate 26 x 31 ?
Standard algorithm for multiplying
26 x 31 = ...
26
31 x
26
78 +
806
We can calculate with other methods:
# Partial Product Method
26 x 31 = ...
26
31 x
6 = 1 x 6
12 = 20 x 1
180 = 30 x 6
600 + = 200 x 3
806
# 26 x 31 = ...
26 = 20 + 5 + 1
then, (20×31) + (5×31) + (1×31) = 620 + 155 + 31 = 806
# Lattice Method
26 x 31 = ...
So, 26 x 31 = 806
Standard algorithm for division
Long Division
133 : 6 = ...
22 Remain 1
6 /133
12 -
13
12 -
1
So, 133 : 6 = 22 1/6
# The other methods
133 : 6 = ...
6 x 10 = 60
6 x 20 = 120
6 x 1 = 6
6 x 21 = 126
6 x 1 = 6
6 x 22 = 132
6×22+1 = 133
So, 133 : 6 = 22 Remain 1
133 : 6 = ...
6 × 10 = 60
6 × 10 = 60
6 × 1 = 6
6 × 1 = 6
(10 + 10 + 1 + 1) = 22
133 = 6 × 22 + 1
So, 133 : 6 = 22 Remain 1
QUADRATICS FORM
Standard form for a quadratic equation:
y = ax2 + bx + c
A quadratic equation is a polynomial function of degree 2, where a, b, and c are all real numbers and a ≠ 0.
Quadratic equations are square. The rate of slope is changing (never same at every point).
Example f(x) = x2 + 4x + 3

Linear equation
y = mx + b
m = slope
b = y-intercept
The gradient is constant and it is in straight line.
Example y = 3x + 1
Langganan:
Postingan (Atom)